使用瞬时频率表示 PM 和 FM 信号

在这篇文章中，我们将探讨相位调制（PM）和频率调制（FM）之间的数学关系。然后，我们将学习如何使用相位调制器来生成 FM 信号，反之亦然。

角调制技术分为两类：相位调制（PM）和频率调制（FM）。系列上一篇介绍了相位调制 ，并提供了一些示例波形，以帮助我们理解消息信号如何影响 PM 波形。现在，从更数学的角度继续我们的讨论，我们将扩展我们的关注范围，包括频率调制。

利用瞬时频率的概念，我们将为这两种信号类型创建数学表示。这将帮助我们探索两种角调制形式之间的关系。我们将发现，PM 和 FM 方法如此密切相关，以至于增加一个电路允许一种类型的调制器生成另一种类型的信号。

PM 波：相位与频率之间的关系

角调制信号可以用一个具有恒定振幅且其自变量（θ）随传输的消息信号变化的正弦函数来表征：

$$=\cos$$

公式 1。

我们将θ称为瞬时角或瞬时相位。在调相（PM）中，瞬时角随消息信号线性变化，产生：

$$=+$$

公式 2.

其中：

fc 是载波频率

kp 是比例常数

m(t) 是消息信号。

图 1 显示了由正弦消息信号生成的 PM 波，载波频率为 fc = 80 Hz，且 kp 的常数值为 25 rad/V。

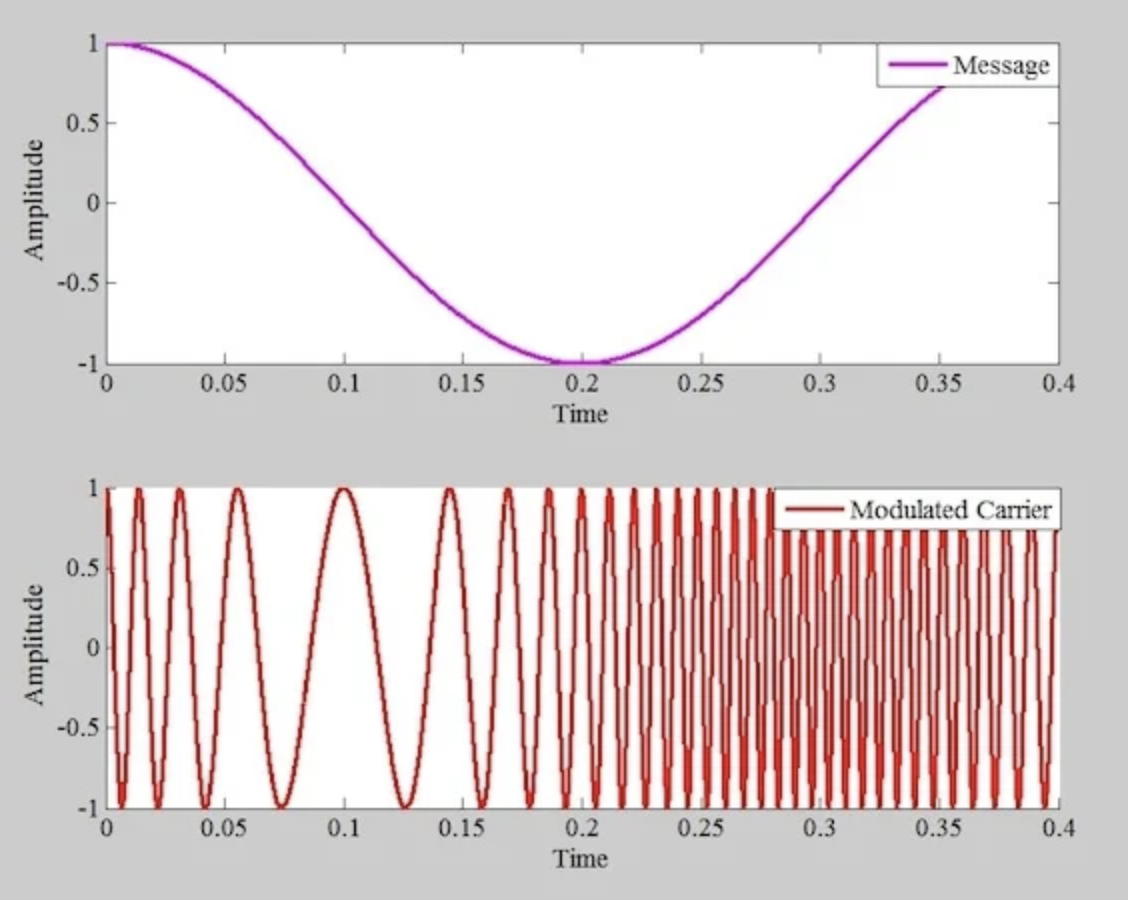
图 1。 一个正弦消息信号（顶部）及其对应的 PM 波（底部）。 

正如我们所见，消息波形下降部分会导致输出频率降低，而上升部分则会增加输出频率。之前的文章提供了几个例子来演示消息信号的上升或下降部分如何影响 PM 波的频率。

另一种看待这一现象的角度是，当消息信号随时间增加时，它会为 2πfct（见公式 2）所贡献的相位项增加一个递增项。因此，调制波的相位会更快地完成一个完整周期。这表现为频率的增加。换句话说，PM 波在 (t) 的正斜率期间被压缩。

相反，当消息信号随时间减少时，它会贡献一个负相位变化，抵消部分由 2πfct 项引起的正相位变化。这意味着调制波需要更长的时间来完成一个完整周期，从而导致频率降低。换句话说，PM 波形在 (t) 的负斜率期间被拉伸。

为了更好地理解这个解释，请考虑以下 fc = 100 Hz 的正弦函数：

$$=\sin +$$

公式3

其中 ϕ(t) 是附加的相位偏差。图 2 显示了该正弦波在三个不同的 ϕ(t) 条件下的一个四分之一周期：

1. ϕ(t) = 0

2. ϕ(t) = 90 – 100t

3. ϕ(t) = 90 + 100t

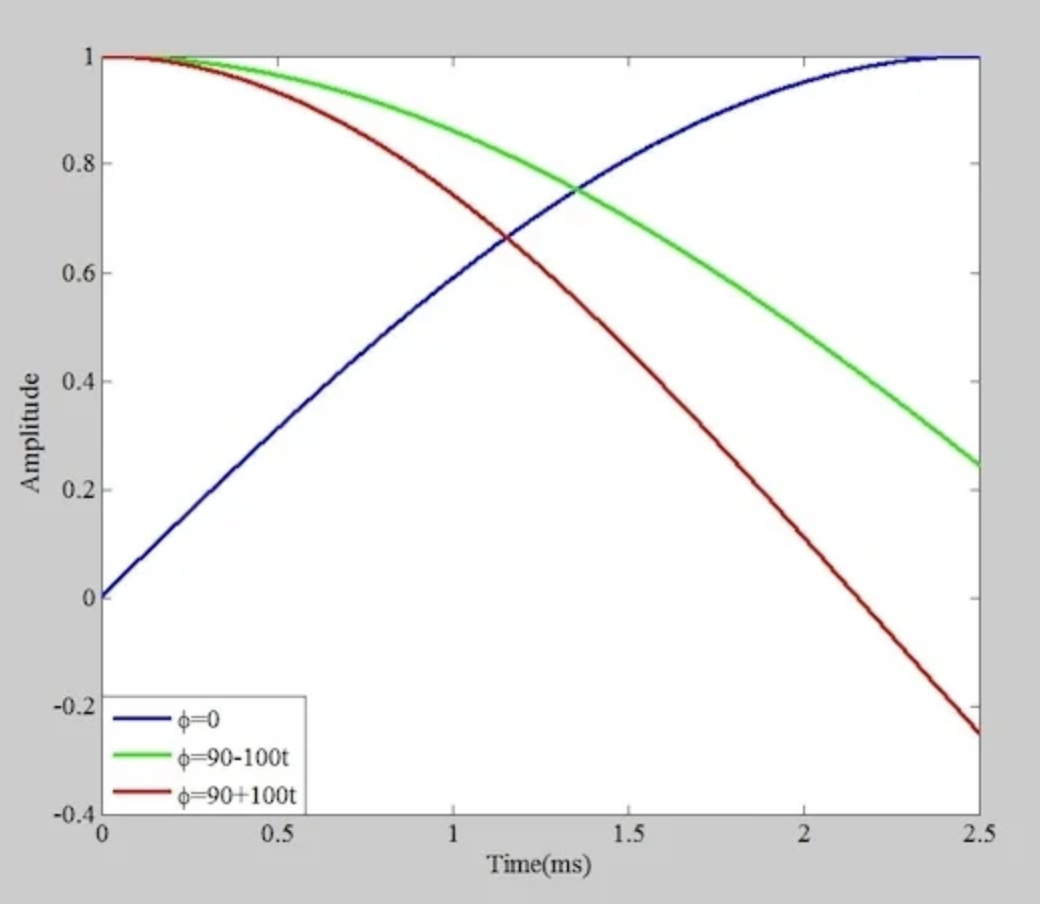
图 2。 由方程 3 描述的波形的一个四分之一周期，对于三种不同的 ϕ(t)。

在上面的图中，蓝色曲线（ϕ(t) = 0）表示一个未调制的波形。对于蓝色曲线，一个四分之一的周期跨越了 0 到 2.5 毫秒的区间。

红色曲线（ϕ(t) = 90 + 100t）表示一个 PM 波形，其中消息信号随时间增长。在这种情况下，来自ϕ(t)的正相位变化增加了来自 2πfct 项的变化。因此，超过一个四分之一的周期适合在 0 到 2.5 毫秒的区间内。

最后，绿色曲线（ϕ(t) = 90 – 100t）表示一个 PM 波形，其中相位项在减少。来自ϕ(t)的负相位变化抵消了部分来自 2πfct 项的正相位变化。结果，波形的一部分不到一个四分之一适合在 0 到 2.5 毫秒的区间内。

瞬时频率

一个未调制的信号，其频率为 fc，振幅为 Ac，初始相位为 ϕ0，可以用一个旋转角速度为 2πfc 的 相量 来表示。这如图 3(a) 所示。一个角度调制的信号相当于一个振幅为 Ac、角速度随时间变化的相量，如图 3(b) 所示。

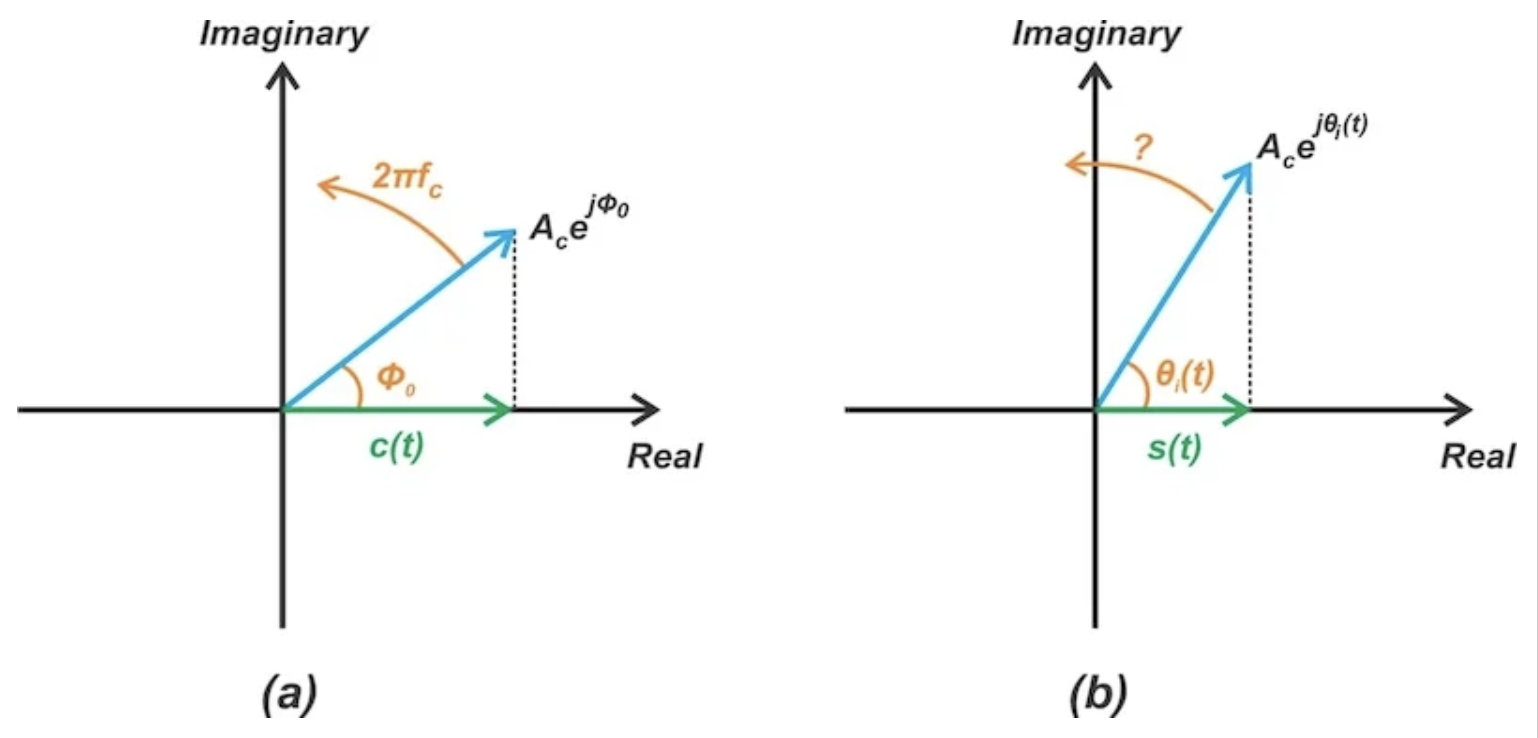
图 3. 未调制信号的相量表示 (a) 和角度调制信号的相量表示 (b)。

让我们更仔细地研究角度调制波。我们如何表征其旋转频率？当 θ 变化 2π 弧度时，相应的相量完成一个完整的旋转周期。因此，在 t 到 (t + Δt) 的时间间隔内的平均频率（单位：赫兹）可以表示为：

$$=+-$$

公式4。

在未调制的载波频率为 fc 且初始相位为ϕ0 的特例中，上述公式产生：

$$=++-+=$$

公式 5。

如所展示，未调制载波的平均频率等于 fc。对于角度调制信号，平均频率取决于所关注时间间隔内消息信号的价值。然而，如果我们让方程 4 中的Δt 趋近于零，所获得的频率可以解释为旋转相量的瞬时频率，f(t)。对于Δt → 0，该方程可以改写为θ的时间导数 ：

$$=$$

公式 6。

根据上述公式，对应相量的角速度等于 2πf(t) rad/s。

通过应用瞬时频率的概念，我们可以解释图 1 中 PM 波的行为。如果我们把方程 2 中的θ代入瞬时频率方程，我们得到：

$$& & +& +$$

公式 7。

这意味着随着消息信号随时间增加，输出频率会上升。相反，当消息信号减少时，输出频率会下降。

表示 PM 和 FM 信号

现在我们已经了解了瞬时相位和瞬时频率的基础知识，我们可以使用它们来对 PM 和 FM 方案提供一个统一的描述。通过将瞬时相位写为：

$$=+$$

公式 8。

其中 ϕ(t) 是相位偏差，我们可以将方程 1 描述的角度调制波表示如下：

$$=\cos +$$

公式9。

这表明瞬时相位是 2πfct 和ϕ(t)所设定的中心值之和。在两种角度调制形式中，ϕ(t)都取决于消息信号。对于 PM，ϕ(t)与消息信号成正比：

$$=$$

公式10。

其中 kp 是比例常数。假设 m(t) 是电压量，kp 以弧度每伏特表示。

由方程式 9 描述的调制波的瞬时频率是通过取瞬时相位的导数来确定的。

$$==+$$

公式 11。

瞬时频率的与消息相关的部分称为频率偏移：

$$=$$

公式12。

在调频系统中，频率偏移与消息信号成正比：

$$=$$

公式13

其中 kf 是频率偏移常数。假设 m(t) 是电压量，kf 以赫兹每伏特表示。

对上述方程进行积分，我们可以确定 ϕ(t) 并将其代入方程 8，从而得到调频信号方程：

$$=\cos +{}^{}m$$

公式14。

注意到上述方程中通常会出现一个常数，这是由于积分产生的。然而，我们假设未调制波的相位在 t = 0 时为零。这消除了常数。

虽然我们正在谈论常数，但值得提一下，比例常数 (kp) 有几个不同的名称。根据你参考的资料不同，你可能会发现 kp 被描述为相位偏移常数、调制器的相位灵敏度、相位调制指数，或者简单地称为调制指数。类似地，kf——频率偏移常数——有时被称为调制器的频率灵敏度。

FM 与 PM 的关系

如果我们建立它们输入之间的特定关系，FM 和 PM 调制器可以产生相同的输出。为了理解这一点，请考虑方程 14 以及下面重述的 PM 信号方程：

$$=\cos +$$

公式15。

从公式14和15可以看出，为了使这两种方法产生相同的输出，需要满足以下关系：

$$={}^{}{}^{}$$

公式16。

where:

mf(t) 是施加到调频调制器的输入

mp(t) 是施加到 PM 调制器的输入。

从公式 16 可以看出，如果 mp(t) 是 mf(t) 的积分，那么 PM 和 FM 电路会产生相同的输出。简而言之，如果我们在一个相位调制器的输入端放置一个积分器，我们可以用它来产生 FM 信号。这个设置如图 4 所示。

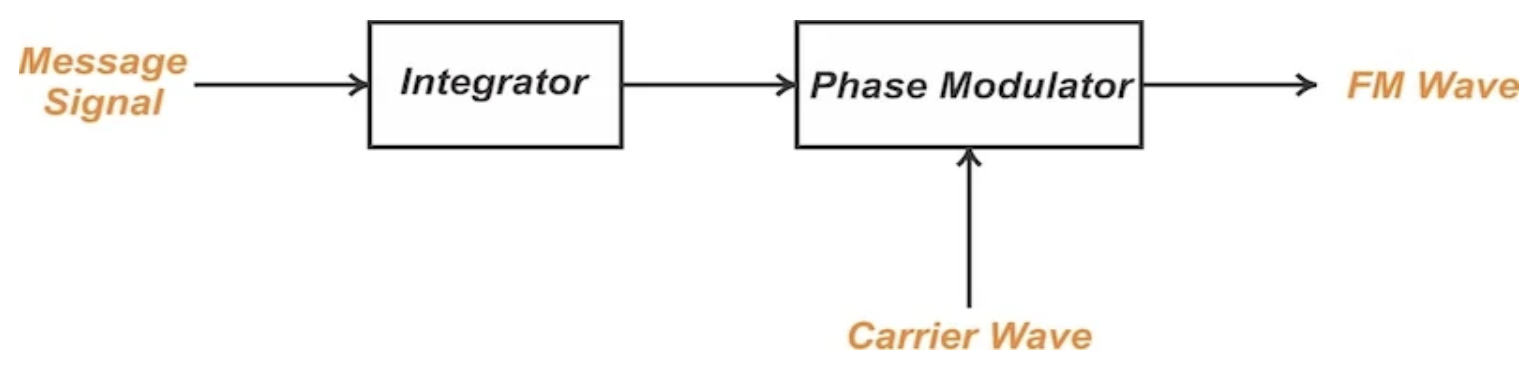
图 4。 使用相位调制器产生 FM 波。

公式 16 还表明，如果施加到 FM 调制器的信号等于施加到 PM 调制器的信号的导数，那么这两种调制器会产生相同的输出。这意味着如果我们对消息信号进行微分，然后再将其用作 FM 调制器的输入，那么 FM 调制器可以用来产生 PM 信号（图 5）。

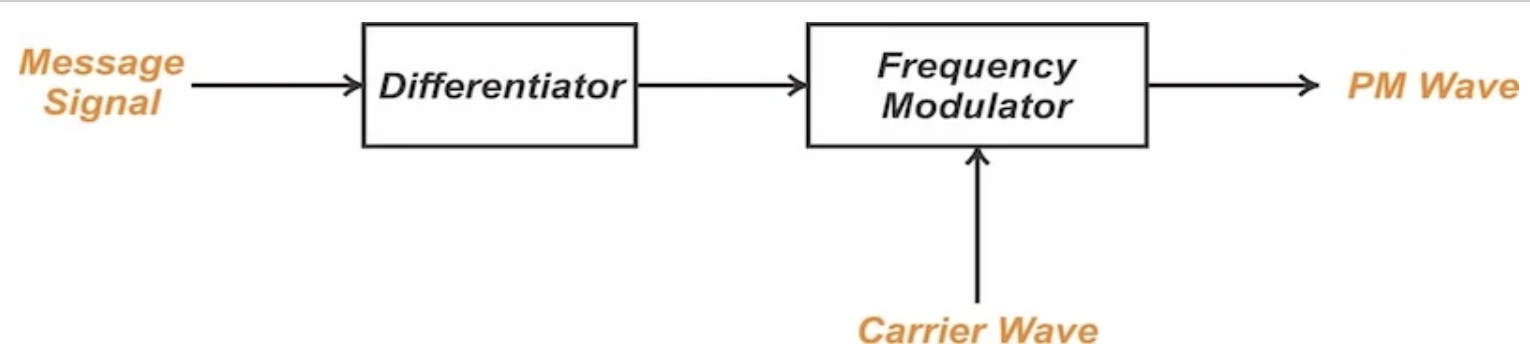
图 5. 使用调频器产生 PM 波。

例如，考虑图 6 左上角所示的正弦波消息 m(t)。

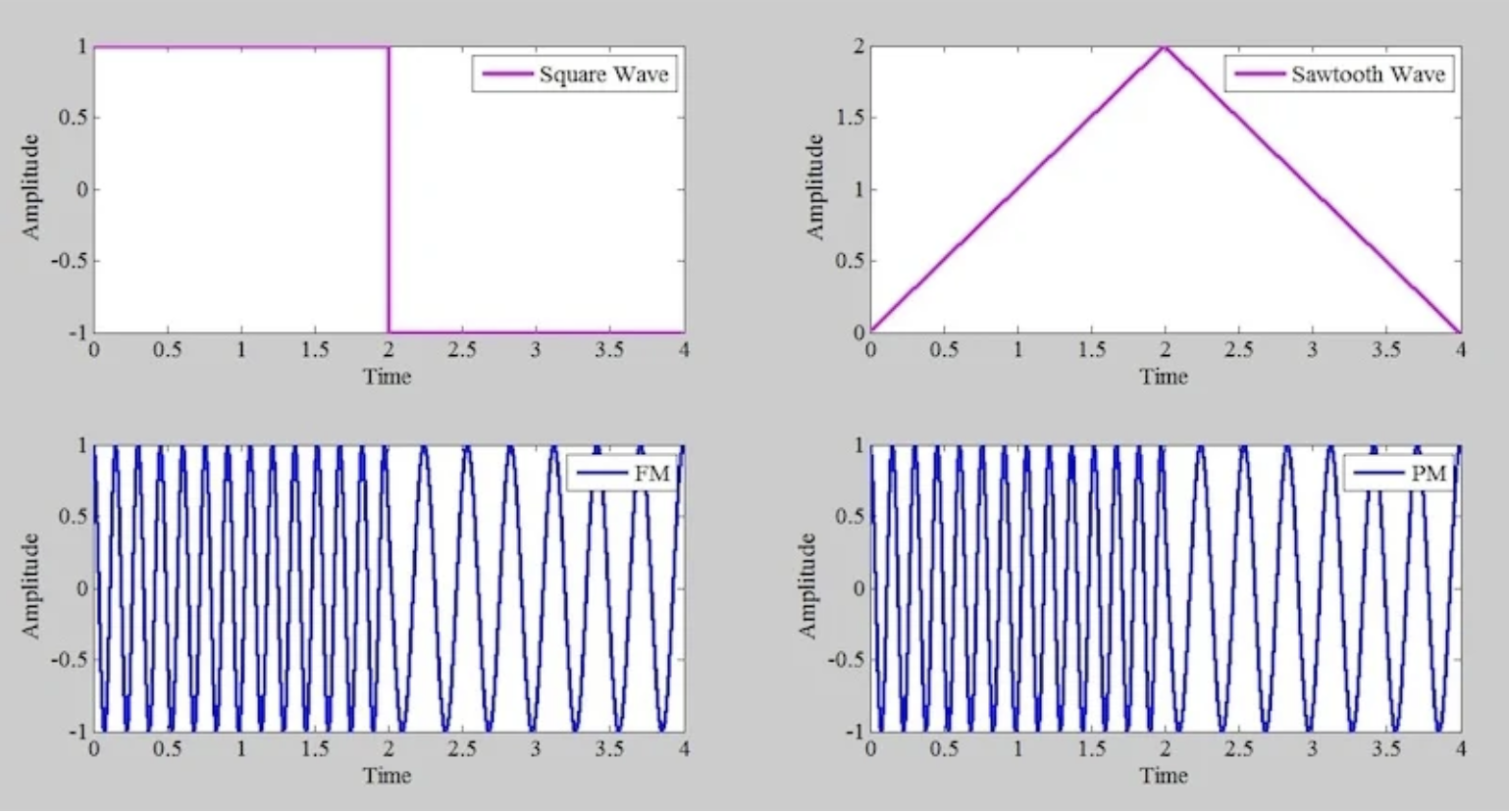
图 6. 左上：一个方波消息信号。左下：其相应的调频波。右上：一个未调制的锯齿波。右下：其相应的 PM 波。

方波消息相应的调频波显示在该图的左下象限中（fc = 5 Hz, kf = 1.59 Hz/V）。该图的右上象限显示一个锯齿波；右下象限显示了其 PM 波，对于 kp = 10 rad/V。

并排放置时，这两个调制波看起来是相同的。由于方波的积分会产生锯齿波信号，这并不令人惊讶。

总结

在这篇文章中，我们通过数学视角深化了对角度调制——包括 PM 和 FM——的理解。我们深入探讨了瞬时频率的概念，并利用这一概念考察了 PM 和 FM 方法之间的密切关系。我希望这篇文章能帮助您更深入地理解这些调制方法以及它们产生的信号时域行为。