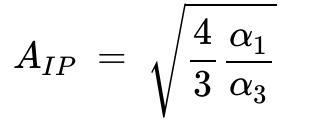理解射频系统中的互调失真和三阶截点

了解双音输入测试如何帮助我们评估射频系统在真实世界信号下的非线性

在本系列的上一篇文章中，我们深入探讨了非线性系统如何对单频输入做出响应。当单频信号施加到非线性系统中时，输出端会出现该频率整数倍频率的谐波分量。这些谐波分量可能位于放大器的通带之外，从而受到严重衰减。在这种情况下，单频测试可能会高估电路的实际线性度。

由于实际电路处理的是由许多频率组成的输入信号，使用两个紧密间隔的频率进行双音测试可以更真实地评估电路的非线性度。它还允许我们检查互调产物，这些是我们称之为输入频率非谐波失真分量的失真分量。即使电路的带宽非常窄，输入音调之间的微小频率间隔也允许我们生成位于电路通带内的失真分量。

在这篇文章中，我们将使用双音输入测试来检查无记忆非线性系统中的互调失真。我们还将学习三阶交点（IP3），这是一个表征这种非线性的重要指标。

双音输入产生的失真成分

图 1 显示了一个具有输入 x(t) 和输出 y(t) 的设备或网络。我们将假设该设备是非线性和无记忆的。

图 1。 一个通用设备或网络。

让我们考察该系统对以下两个音调输入的响应，该输入包含频率分量 ⍵1 和 ⍵2：

$$=\cos +\cos$$

公式 1。

为了简化，我们假设这两个音调的振幅均为 A。

如果电路是无记忆的，我们可以使用多项式表达式来近似其输入输出特性：

$$\approx +++++..$$

公式 2.

多项式表达式中的项 ⍺1 代表线性系数，它放大输入信号而不产生失真。将输出信号的这一部分表示为 y1(t)，我们有：

$$=\cos +\cos$$

公式3

我们通常保留多项式表达式中的项直到三阶项，我们将在本文中保持这一做法。

二阶项

二阶项，由系数 α2 表示，产生如下输出电压：

$$& \cos +\cos & +++\cos ++\cos -$$

公式4。

从公式4中，我们观察到二阶项在以下频率上产生能量：

• 直流电。

• 输入音调的第二谐波（2ω₁ 和 2ω₂）。

• 差频（|ω₁ - ω₂|）。

• 和频(ω₁ + ω₂)。

图2显示了二阶项产生的频率分量。为简化起见，仅显示了正频率。

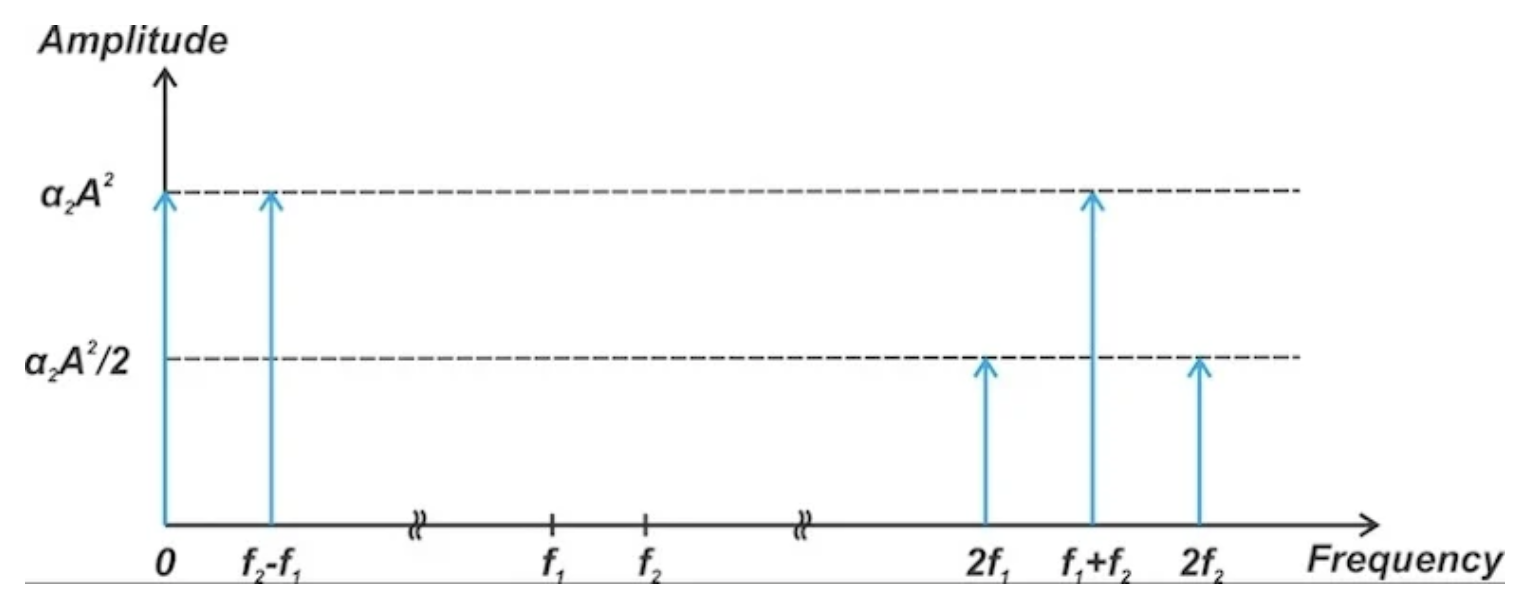
图 2。 二阶项产生的失真产物。

图2证实，该电路在双音输入时产生互调产物——这些不是输入频率谐波的失真分量。

请注意，余弦项（如 Acos(⍵t))的频谱由两个冲激组成，一个在⍵，一个在–⍵。每个的幅度为 A/2。尽管电路被 f1和 f2 的信号激励，但具有二阶非线性的电路输出频谱在这些频率上没有任何信号分量。

三阶项

接下来，让我们考察由三阶项产生的互调产物：

$$& \cos +\cos & \cos +\cos +\cos +\cos +\cos ++\cos -+\cos ++\cos -$$

公式 5。

三阶项在基频（⍵1 和⍵2）、三次谐波（3⍵1 和 3⍵2）、2⍵1 ± ⍵2 以及 2⍵2 ± ⍵1 处产生能量。这些频率分量如图 3 所示。

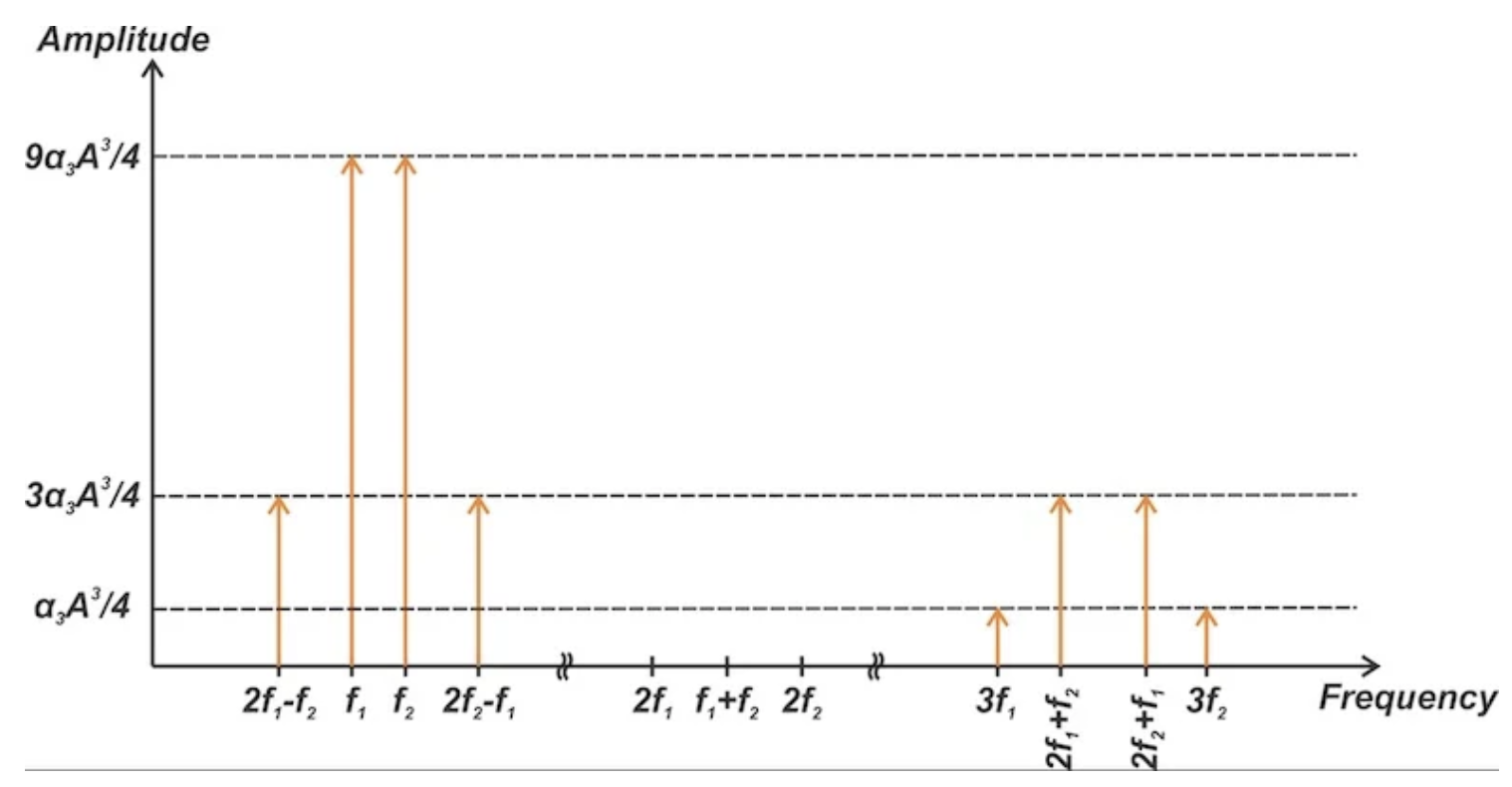
图 3。 由三阶非线性产生的失真分量。

三阶失真不会在二阶失真分量存在的频率处产生能量。

失真产物的全范围

图4结合了图2和图3，以获得由三阶表达式产生的完整范围失真产物。

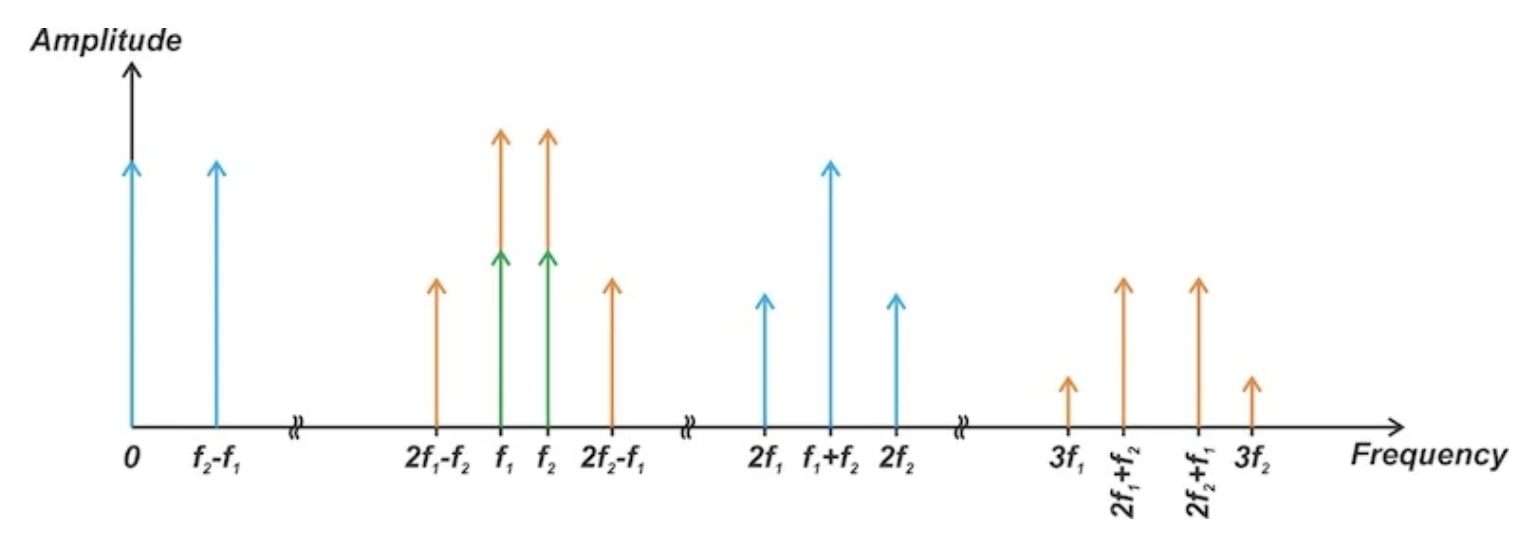
图 4。 当输入输出特性由三阶表达式建模时，线性项（绿色）、二阶项（蓝色）和三阶项（橙色）产生的频率分量。

请注意，该图仅用于显示不同组件的存在及其发生频率。组件的相对幅度取决于电路的非线性特性，这里并不关注。

在我们继续之前，值得提到的是，我们可以为形式为 m⍵1 + n⍵2 的每个失真产物分配一个阶数，其中阶数定义为 |m| + |n|。根据这个定义，在 2⍵1、2⍵2、⍵2 – ⍵1 和 ⍵1 + ⍵2 处的互调产物都是二阶的。

窄带系统可以抑制失真分量

如图 4 所示，一个三阶非线性特性会产生多种不同的失真产物。这些产物从直流到三次谐波不等。如果这些失真分量足够位于电路的通带之外，则可以大大抑制它们。

这在带宽很窄的射频电路中尤其重要。如果电路在基波分量周围的带宽很窄，那么电路的带通响应将衰减以下所有频率处的失真产物：

• <强 id=0>差异项： ⍵<下标 id=1>2 – ⍵<下标 id=2>1

• 和项： ⍵1 + ⍵2

• 谐波项： 2⍵1, 2⍵2, 3⍵1, 3⍵2

• 互调项： 2⍵1 + ⍵2,2⍵2 + ⍵1

对带外失真分量的衰减可以使电路看起来比实际更线性。然而，即使电路带宽非常窄，由两个靠得很近的频率组成的输入信号也可能产生带内失真分量。确定这些失真项使我们能够评估电路的线性度。

如图 4 所示，2ω₁ – ω₂和 2ω₂ – ω₁的失真分量在频率上非常接近基波分量（ω₁和ω₂）。这些互调产物，我们将在本文余下部分中称为 IM3 分量，是我们特别感兴趣的部分。

互调失真指标

考虑三个蓝牙设备分别以 f1 = 2.41 GHz、f2 = 2.42 GHz 和 f3 = 2.43 GHz 发射。注意到 2f2 – f3 = 2.41 GHz，我们观察到在 2.42 GHz 和 2.43 GHz 发射的信号可以为工作在 2.41 GHz 的接收设备产生 IM3 成分。

这些 IM3 成分对射频系统构成了重大挑战。拥有一种量化这种效应的方法，以便我们能够评估和比较不同系统的线性度，是至关重要的。一个指标是互调失真比（IMR），它定义为其中一个互调项的幅度与期望输出信号幅度的比值：

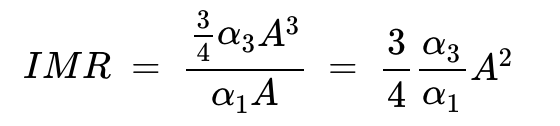
公式 6。

这种线性度指标的一个重要局限性是它与信号电平有关。在比较系统时，我们理想情况下需要一个仅是电路参数函数的指标。为了解决这个问题，我们使用三阶交点（IP3）指标。

考虑图 5，它展示了基波输出和 IM3 分量的功率如何随输入功率变化。

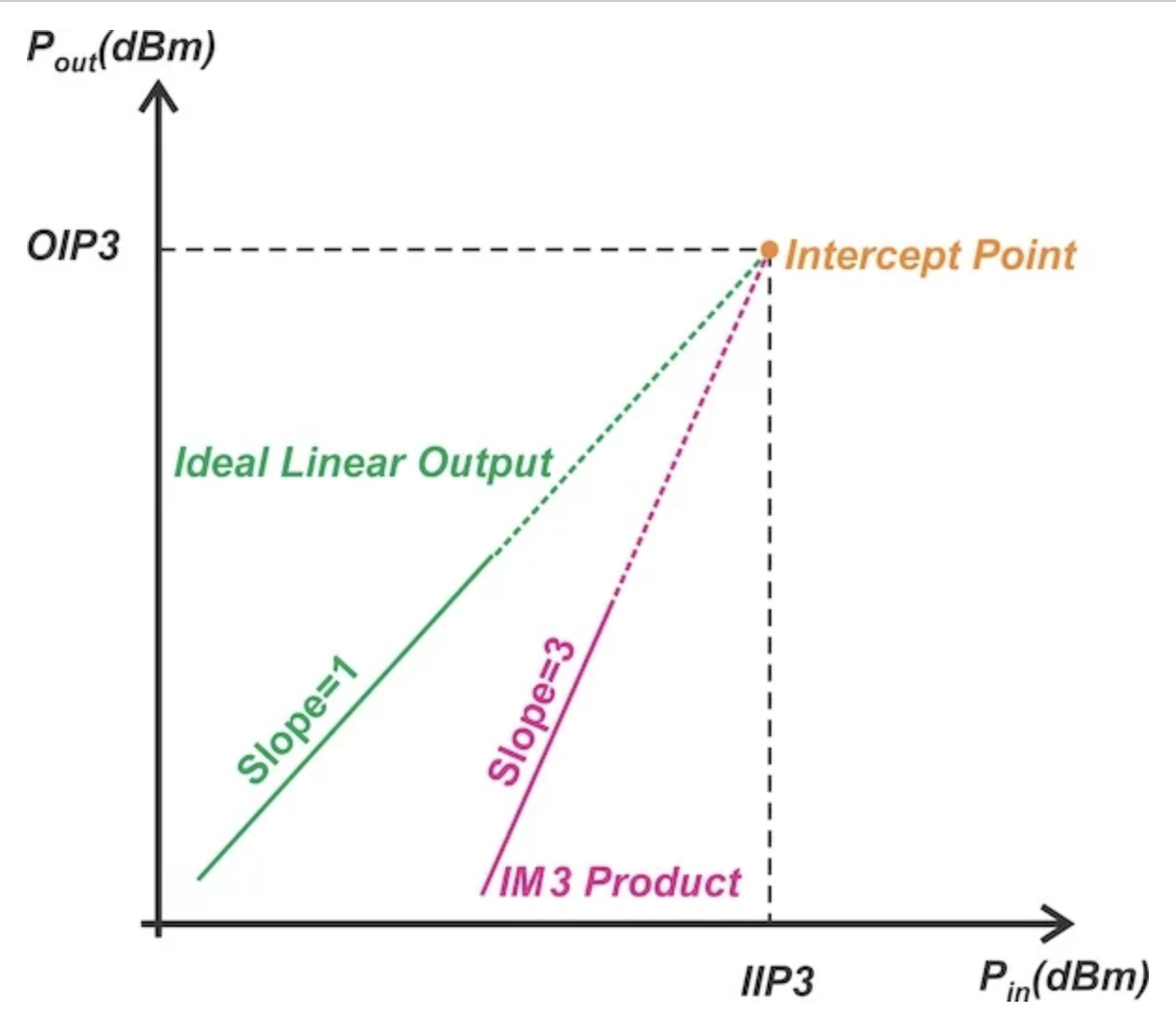
图 5。 三阶交点。

虽然基波分量表现出 1:1 的斜率，但 IM3 分量每增加 1 dB 的输入功率就会上升 3 dB。这是因为基波输出分量与 A成正比，而 IM3 产物与 A3 成正比（见公式 5）。

即使三阶交调失真（IM3）分量在低输入功率时非常小，但由于它们与输入幅度 A 的三次方关系，会随着输入幅度的增加而迅速增长。因此，如果我们持续提高输入功率，理论上应该存在一个点，使得基波和三阶交调失真（IM3）产物的功率相等。

这就是我们所说的三阶交调点。在上述图中，它被标记为橙色。交调点处的输入功率和输出功率分别用 IIP3 和 OIP3 表示。

确定 IP3 点

实际上，在输入功率较高时，基波和 IM3 组件都表现出 压缩 ，如图 6 所示。

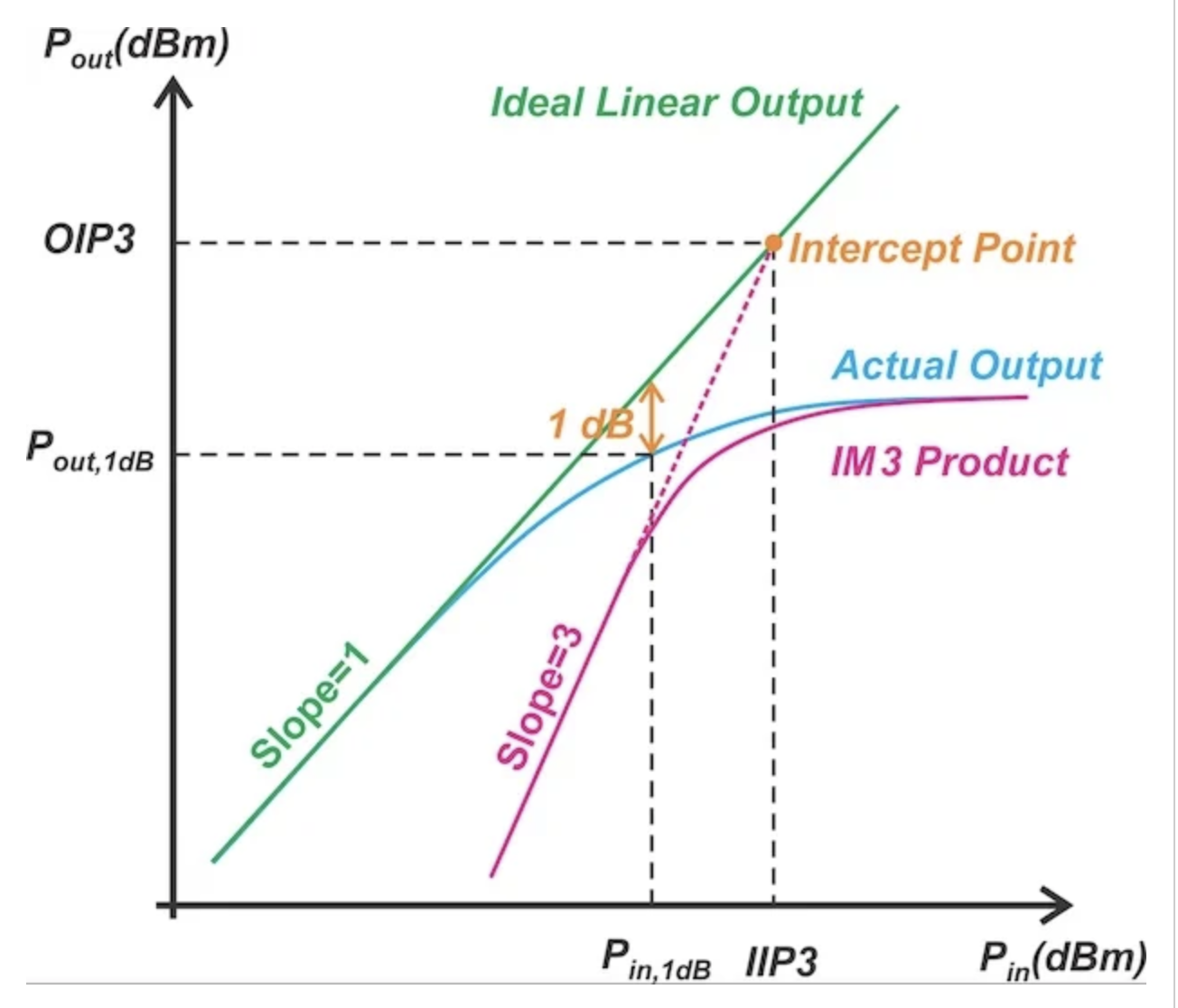
图 6. 具有增益压缩的系统的三阶交点。

IP3 不能直接测量。相反，它是通过从其线性工作区域外推基波和 IM3 功率曲线，并找到交点获得的。如上所述，这是 IM3 分量振幅等于基波输出分量振幅的点。通过应用这个定义，我们可以建立 IP3 点处信号振幅与三阶多项式逼近系数之间的关系。

根据公式 5，IM3 分量的振幅为：

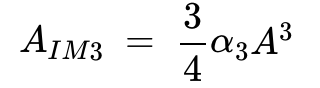
公式 7。

同时，基波输出分量的振幅为：

$$=$$

公式 8。

如果我们设 AIM3 等于 Afund 并求解 A，我们得到对应于 IP3 点的输入幅度（AIP)：

公式9。

如果我们知道系数α₁1 和α3，我们可以使用上述公式来确定对应于 IP₃点的输入信号幅度。

总结

在这篇文章中，我们研究了当双音输入施加到一个无记忆的非线性系统时会发生什么。当我们使用多项式近似来表示这个系统时，我们看到输入频率分量被高阶多项式项混合（相乘）。这产生了在非输入谐波频率处的互调失真（IM3）分量。我们重点关注了第三阶失真项在 2⍵1 – ⍵2 和 2⍵2 – ⍵1，因为这些频率通常非常接近基本分量⍵1 和⍵2。

为了量化 IM3 分量，我们使用三阶截点（IP3）指标。三阶截点（IP3）点是衡量系统非线性的指标。它使我们能够评估系统在存在与所需信号频率接近的大幅度干扰信号时接收弱信号的能力。